1 1. Introduction and background to Griffith’s theory
http://ajaytaneja-historydevpfracturemech.blogspot.co.uk/
i.
Similar
to surface tension in liquids, all solids are associated with surface energies
which develop because all atoms close to the surface behave differently from
the atoms in the interior of the solid.
ii.
Griffith
realized that a crack in a body will not grow until energy is “released”
to suffice for the energy that is required to create 2 new surfaces: one above
and one below the crack plane.
Figure: Plate with a
central crack
In
the last section of the above article, a plate with fixed ends with a central
crack was considered and an expression for “Energy release rate” was formulated
for the specific example.
The
aim of this article is to;
·
Firstly,
arrive at the mathematical formulation of the energy release rate. It should be
noted that the expression for the energy release rate in the preceding article
stated above, was developed for the specific case of a plate with a central
crack with fixed ends. Thus, in section 2 a generic formulation for energy
release rate is obtained.
·
Section
3 aims at providing a physical insight to the reader considering the progress
of crack growth in brittle materials.
·
Then,
in section 4 and section 5 of the article, expressions for the energy release
rate are derived for 2 respective extreme cases;
a)
Constant
load case
b)
Constant
displacement case
The
main reason to discuss the extreme cases is to make aware that energy required
to propagate the crack can be from different sources. In the case of constant
load case (as discussed in section 3), the energy requirements for crack
propagation are met through the external work done on the system which results
in an overall increase in the strain energy stored in the structure. It should
be realized through the section on “constant load case” that part of the
external work done on the system goes on to increase the strain energy stored and
a part of it is used for crack propagation.
In
case of “constant displacement” case, the strain energy of the system is
reduced owing to its contribution to crack propagation. In a “real” practical
scenario, the energy contribution to crack propagation is a mix of “constant
load” and “constant displacement”.
2 2. Mathematical formulation of energy release rate
With an advancing crack, the following happens in a general case;
2 2. Mathematical formulation of energy release rate
With an advancing crack, the following happens in a general case;
i.
The
stiffness of the component decreases.
ii.
The
strain energy of the system might increases or decrease. This has been
discussed in length in section 4 of this document.
iii.
Energy
is consumed in creating two new surfaces.
Mathematical
formulation of energy release rate is carried out by invoking the law of
conservation of energy. Consider the case of increment in crack area ∆A. This
causes an increase in crack growth, an incremental external work ∆Wext
is done by the external forces and the strain energy in the body of the
component increases by ∆U.
That
is;
If
there is an incremental external work done = ∆Wext
Then;
Part
of is stored in the system as strain energy = ∆ U
Part
of it is used in incrementing the crack surface area by ∆A
Now,
‘G’
is the energy release rate which is defined as energy available per unit area
Re-organizing;
1 3. Progress of crack growth in brittle materials
1 3. Energy release at constant load
1 4. Energy release at constant displacement
As the crack grows, moves
with a velocity, there is also kinetic energy imparted to the cracked portion
of the body. This has not been considered in the discussion above.
1 3. Progress of crack growth in brittle materials
Crack resistance:
For
a crack to grow, the crack resistance “R”, is the energy required by the crack
per unit increase in area. It characterizes the material behaviour. A minimum
value of “Ri” is needed to make the crack to grow. The crack resistance “R” is
the inherent property of the material.
Crack resistance: brittle materials
For
a brittle material, wherein no plastic deformation occurs, ‘R’ remains constant
as shown below;
Figure: Crack resistance in a brittle material
It
should be noteworthy at this stage, that in case of brittle materials, as
described through Griffith’s theory, once the crack resistance is reached i.e.
once the energy required to form 2 new surfaces is available, the crack growth is spontaneous and failure
catastrophic. This is now justified, as the crack resistance in a brittle
material remains constant and once this is reached, crack starts growing on its
“own”.
In
the sub-sections that follow, we graphically represent the progress of crack
growth with increasing stress level.
Graphical representation of conditions
of fracture of a brittle material
In
the above section, it was mentioned that the crack resistance ‘R’ in case of a
brittle material remains constant. Let us look at the graphical representation
of the conditions of fracture of a brittle material.
On
the positive side of the x axis, is marked the incremental crack growth. On the
negative side, is shown the initial crack. ‘R’ is the resistance which as
discussed in the section is constant for brittle material because there is no
contribution to the increase in resistance from the plastic deformation (as the
material, it does not plasticize). Let us examine the variation of ‘G’ with
stress σ and increasing crack length ‘a’.
If
we apply a stress which is sufficiently small and if we plot the energy as a
function of crack length, the curve of G (which varies linearly with ‘a’) will
lie below ‘R’. Thus, the energy released is not sufficient for the crack to
grow: the crack will thus remain stationary.
See
figure below:
Figure: Variation of ‘G’ with stress σ and the
crack length ‘a’
Next, if we increase the
stress to σ1, which is still not “critical” since the energy
released is less than the resistance: “R”.
Figure: Variation of ‘G’ with crack length (the
plate being stressed to σ1)
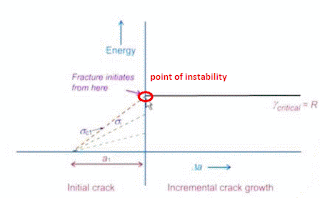
If the stress,
is increases to σc1(this stress is termed as the ‘critical stress’
because as this stress, the energy released is equal to the energy required to
form 2 new surfaces), then, G=R and the point of instability occurs as shown in
the figure below;
Figure:
Fracture initiation (point of instability) when ‘G’ = ‘R’
It should be
noted that the behaviour of the structure upto the point of fracture initiation
as mentioned above remains the same in all brittle materials. Beyond the point
of fracture initiation the crack propagation starts and fracture is
catastrophic in brittle materials.
We shall now
see the sources of energy for formation two new surfaces: one above and one
below the crack plane. Two extreme cases of constant load and constant
displacement will be discussed in considerable detail.
1 3. Energy release at constant load
Consider
the load on the component is such that the material begins to tear, extending
the crack by δa, where δa is small relative to ‘a’. During the crack extension,
the load “P” is kept constant. With the extended crack, the component is less
stiff, so, for the same force “P”, the displacement of the component is larger
by δΔ. The internal strain energy is then,
as
shown in the figure below.
Figure: (a) A component with crack growth δa
subjected to load P (b) Load displacement curves for components with crack
lengths a and a+δa, subjected to the same load P.
The
increment of work done by the constant load P as the crack extends is:
δW = PδΔ
The
change in the internal strain energy of the component is;
Hence,
half of the work done by the load P is used to increase the internal strain
energy of the component, which leaves an excess energy δE of:
This
energy is used to extend the crack: i.e. to break the atomic bonds to create
two new surfaces- one above and one below the crack plane.
Thus, the energy release rate per unit
area of the new crack surface is;
G’
is the energy release rate which is defined as the energy available per unit
area (kJ/m2) to grow a crack of width ‘B’ by distance δa. If the
calculated value of ‘G’ exceeds the material toughness Gc the crack will grow.
1 4. Energy release at constant displacement
Consider
now a scenario when the load on the component is such that the material begins
to tear, extending the crack by δa, where δa is small relative to a. During
crack extension, the displacement Δ is constant. With the extended crack, the
component is less stiff, so for the same displacement Δ, the required force is
changed by δP. The internal energy is then;
as
shown in the figure below.
Figure:
(a) A component with crack growth δa subjected to constant displacement (b)
Load displacements curves for components with crack lengths ‘a’ and ‘a+δa’
subjected to the same displacement Δ
The
system with a larger crack is less stiff, so δP is negative.
Since
Δ is constant, the increment of work done by the applied load is δW = 0. The change
in the internal energy of the component is;
Hence,
the energy available to be released from the component to extend the crack is;
Note
that δP and thus δU is negative. So, δE is positive
The
energy release rate per unit area of the new crack surface is:
G’
is the energy release rate.
Interpretation of constant load and
constant displacement cases:
It
might be noted that the above mathematical discussion considering the cases
involving: constant load and constant displacement might look a little abstract
and too theoretical. The main emphasis of the discussion is to realise that a
source of energy is needed for crack propagation and that source can be either
from:
a)
an
external work done on the system. And, whenever there is work done on the
system strain energy is stored in the system. In order for the crack to
propagate, a part of the energy due to the work done is used up in increasing
the overall strain energy stored in the system and a part of the energy is
released to aid in crack propagation.
b)
when
there is no external work done on the system (i.e. constant displacement case),
then the source of energy for crack propagation comes from a decrease in the
overall strain energy of the system
The
cases involving constant load and constant displacement are cases for pure
theoretical interest and according to me; the engineer need not attempt to
physically imagine the scenarios. This is my personal point of view. From a
practical point of view, the energy needed from the crack to propagate comes
from a mix of reduction in strain energy of the system and through the work
done on the system.
As the crack
grows, moves with a velocity, there is also kinetic energy imparted to the
cracked portion of the body. This has not been considered in the discussion
above.

















No comments:
Post a Comment